1/19 :: 실강

회귀

포아송 프로세스

GLM

 

Clustering 군집화

 

Q. 선형회귀말고도 푸아송분포 같은 분포개념이 필요한 경우가 있나요?

A. 엄청 많다. F분포(통계 유효성 검증), 카이제곱 분포(독립성 검증) 등 선형회귀 말고도 많이 쓰임

 

 

비슷한 관측치끼리 묶는 비지도학습

비슷하다? 거리Distance, 특히 유클리드 거리 사용

 

 

Normalization 정규화

 

 

다른 방법도 있지만, 원래 수치가 아닌 다른 수치를 사용해야한다는 것은 동일하다. 

 

 

K-means 학습

 

b) 먼저 x좌표를 랜덤하게 잡는다

c) 랜덤 할당된 데이터와 가까운 순서대로 설정

d) 해당 군집의 평균을 계산해서 다시 x 좌표 할당

..

수렴할때까지 반복한다. 

 

ex) Nearest Neighbor

 

 

cf) k-means는 변화하는데 계속 바뀌면 안되니까 룰로 정의한다? 더 알아봐야한다. 

 

 

 

https://en.wikipedia.org/wiki/Medoid#:~:text=Medoids%20are%20representative%20objects%20of,members%20of%20the%20data%20set

Medoid - Wikipedia

K-means의 변형으로, 항상 정답은 아니다

 

 

 

 

K-mens 의 한계 1 : 다양한 데이터

 

 

K-mens 의 한계 2 : 다양한 데이터

 

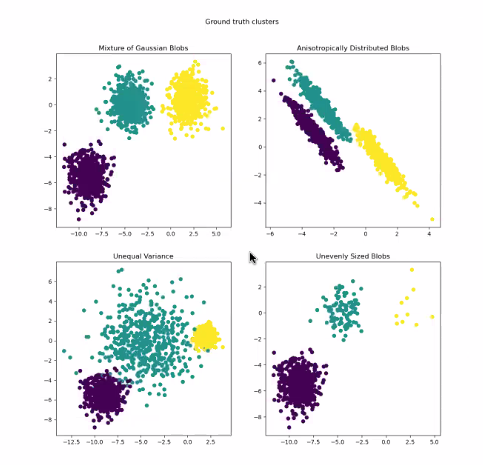
해결법? Covariance 공분산 학습

 

 

 

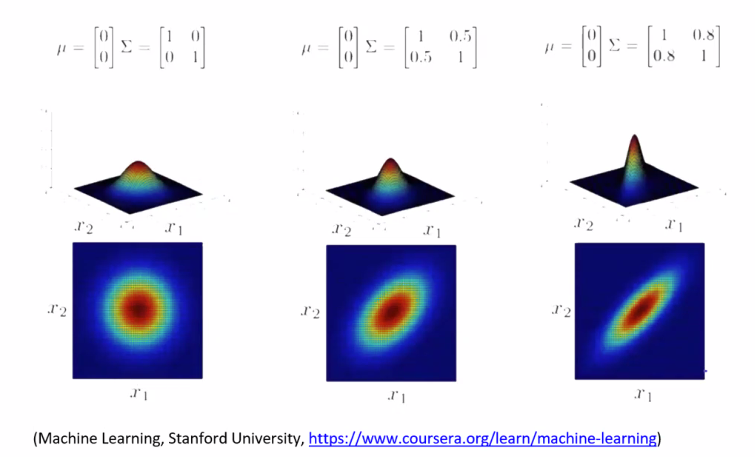
GaussainMixture 가우시안

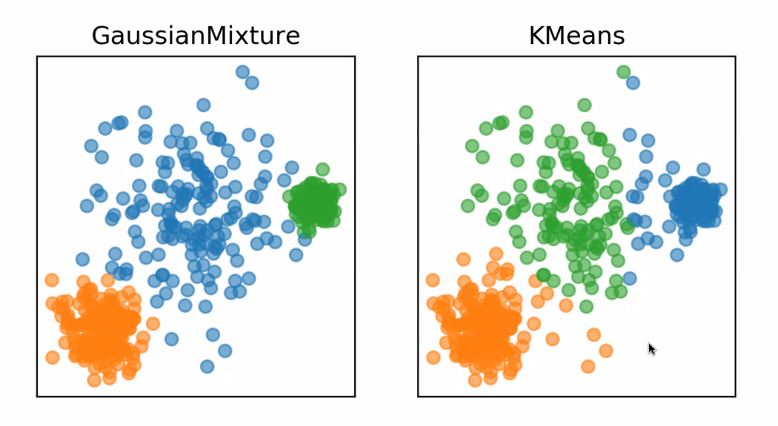
여러 분포가 섞여있을 때 ? 

 

 

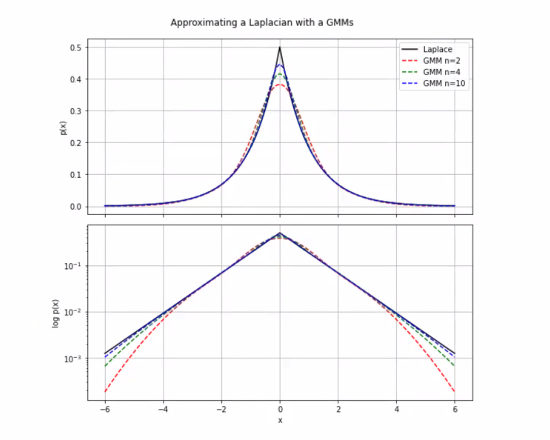
GMM

 

 

 

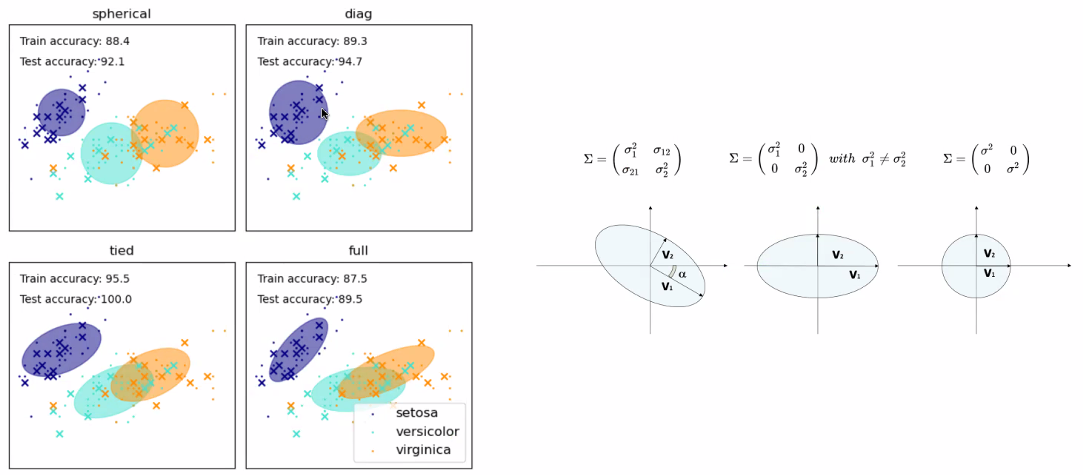
LMM : Laplace Mixture Model

 

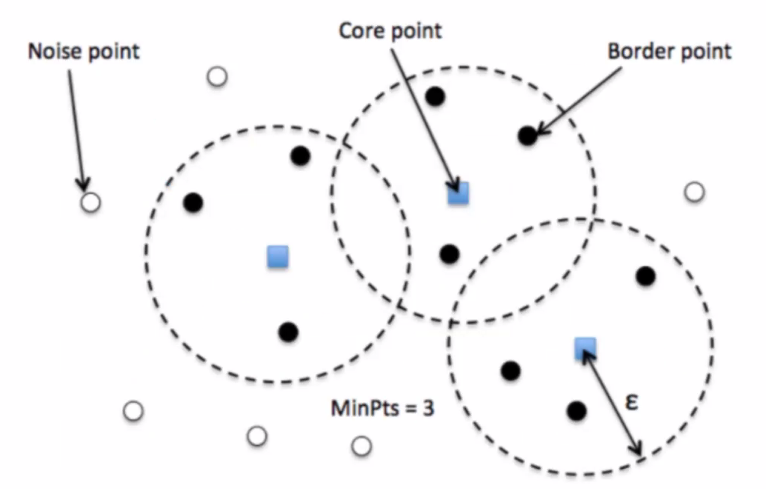
DBSCAN : 이상치 특정용으로 많이 썼었음

 

 

수학에서 CS로 행렬 분해

 

차원의 저주 : 차원이 증가할수록 가까운 애들이 사라짐

 

 

넘어야하는 pca 수학의 장벽

 

 

 

 

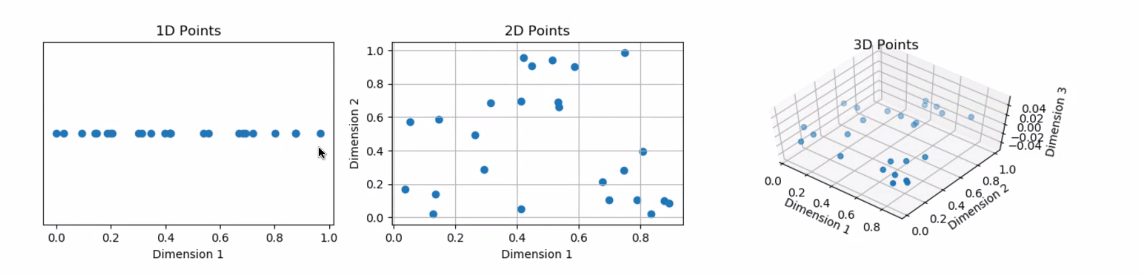
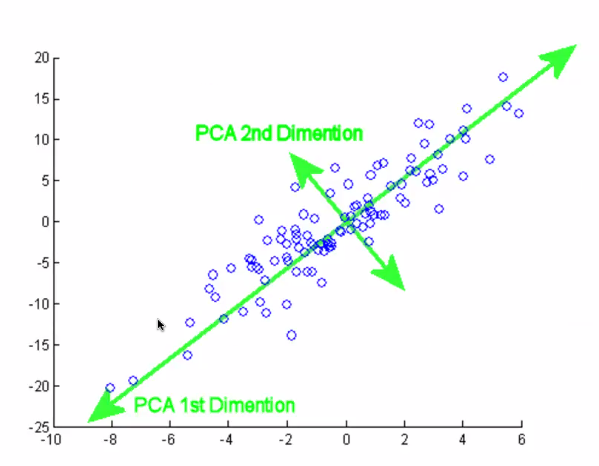
데이터의 크기를 압축한다고 생각하면 편함

 

 

 

SVD : Netflix prize

 

 

 

PCA vs SVD

 

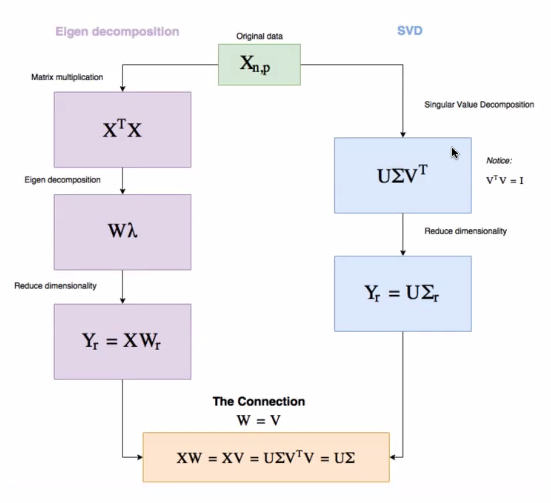
행렬분해 

 

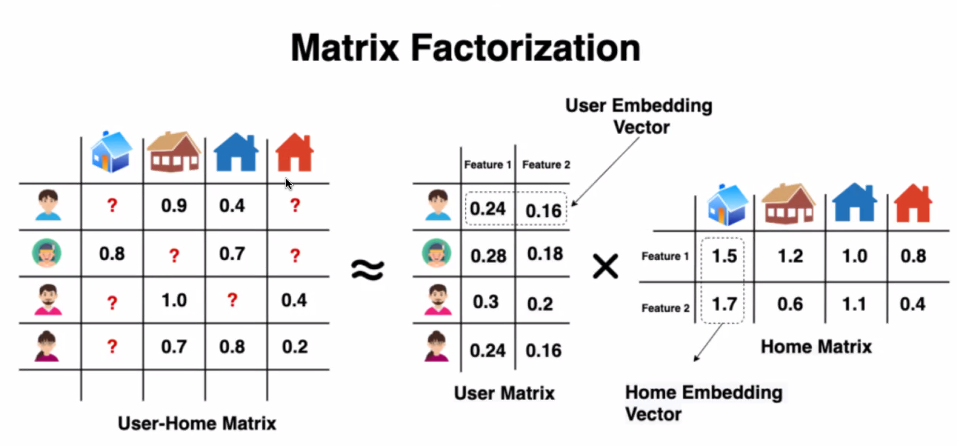
차원을 축소했다가 다시 펼치면 값들이 채워짐

 

유저에 대한 imbedding vector와 item에 대한 imbedding vector가 따로 생성됨

축소했다가 펼치는 과정에서 얼추 값들이 입력됨

 

 

PCA ,SVD의 한계 : 최적화

빈 matrix를 만들고 하는 과정에서 소요가 큼

 

공간적으로 압축하는 예시

 

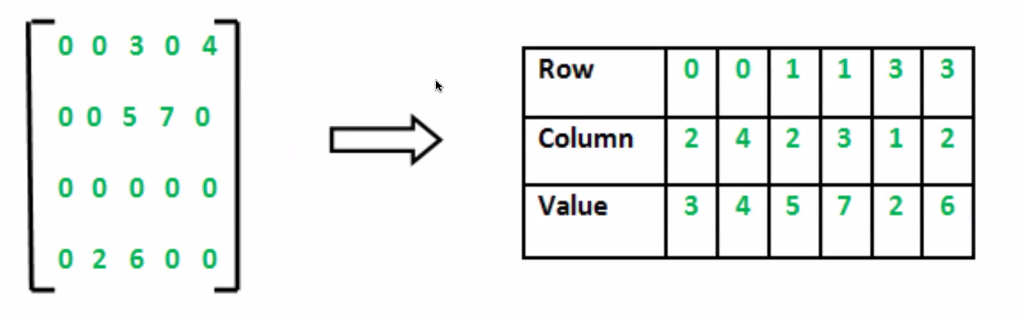
Alternative Least Square

 

 

Neareest Neighbor : Annoy

 

 

실습

 

정량적 접근 뿐만 아니라 정성적 접근도 고려

 

rule 기반으로 하면서 조금씩 고도화해가는 것이 중요함

 

과정을 진행하면서 잘되가는지 살펴보는 것 

 

모든 코드를 다 짤필요는 없고, 가져와서 입맛에 맞게 변형 및 가공 등 수정을 거치면서 사용

 

2000개 정도면 anova 검정하기 좋음

 

 

Q. pandas를 쓰다보면 데이터가 너무 클 때 느려서 한계를 느낀다.

A.  아래 사진 참고 

https://drive.google.com/file/d/12faqaslFIF-Sg_sU3jeGyauW5ClRqS8D/view

 

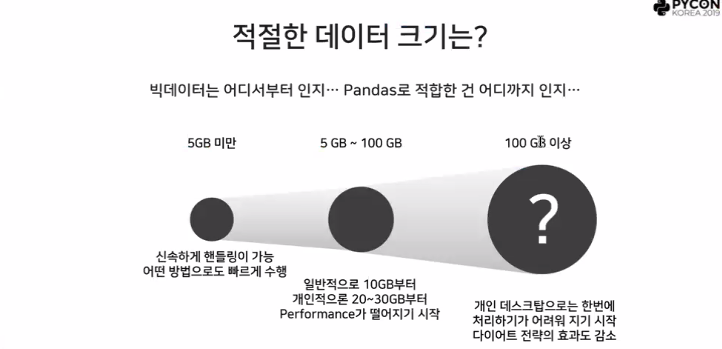
추천, 스파크 관련

https://www.google.com/search?q=agawal+recommender+system&rlz=1C5CHFA_enKR1070KR1070&oq=agawal+recommender+system&gs_lcrp=EgZjaHJvbWUyBggAEEUYOTIJCAEQABgNGIAEMggIAhAAGA0YHtIBCDQxNjJqMGo5qAIAsAIA&sourceid=chrome&ie=UTF-8

🔎 agawal recommender system: Google 검색